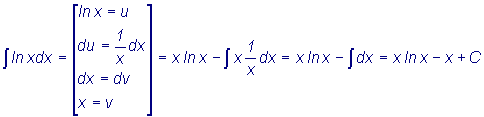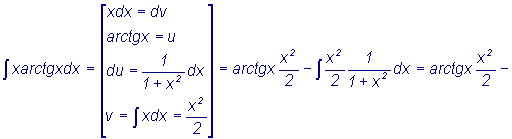Lect 4.2.2.

Темы \| Предыдущий пункт \| Следующий пункт \| Литература

Лекция 4.2. Методы интегрирования

4.2.2. Интегрирование по частям

Представим подынтегральное выражение f(x) в виде двух множителей f(x)dx = u(x)^.v(x)dx. Пусть u(x) и v(x) функции аргумента x, имеющие производные u^I и v^I . Согласно правилам дифференцирования

, значит исходя из свойств интеграла 2 и 4

т.к. u^Idx=du , а v^Idx=dv то

Получаем формулу интегрирования по частям.

Применять ее целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. Отметим, что в некоторых случаях данную формулу необходимо применять несколько раз. Этот метод интегрирования рекомендуется использовать, когда имеется произведение алгебраического многочлена на одну из следующих элементарных функций:
1. Тригонометрические функции ( sin x, cos x );
2. Трансцендентные функции ( e^x , ln x );
3. Обратные тригонометрические функции ( arcsin x , arctg x и т.д.).

Порядок применения формулы интегрирования по частям:

1. Выбор u и dv ;
2. Нахождение du (du=u^Idx) и (как интеграл от v(x) без учета постоянной С).
3. Применение формулы интегрирования по частям.

Поскольку под знаком интеграла стоит обычно произведение 2-х функций, то иногда бывает трудно сделать выбор u и v . В этом случае можно воспользоваться простым правилом.

Правило:
а) В качестве функции u выбирается та из функций, которая при дифференцировании упрощается больше.

Пример:

Рассмотрим
(x+1)^I=1, (sin x)^I= cos x. Очевидно, что первая из функций упрощается при дифференцировании больше, поэтому следует выбрать u=x+1.

б) Если невозможно сделать очевидный выбор в пользу функции u, то в качестве v выбирается та из функций, которую легче внести под знак дифференциала.

Формула интегрирования по частям может применяться неоднократно, но всякий раз используются одни и те же правила.

Рассмотрим несколько примеров применения формулы интегрирования по частям.

Примеры:

Интеграл, приводящийся к исходному.

Это частный случай применения формулы интегрирования по частям, когда в результате мы получаем выражение I=uv-aI, где

, а I - исходный интеграл. Тогда получаем, что

Пример:

т.е. получим исходный интеграл I с коэффициентом

Задачи для самостоятельного решения.