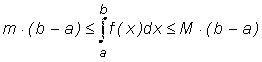| Темы | Предыдущий пункт | Следующая лекция | Литература | |
|
|
|

Определённый интеграл. Основные понятия. |
|
|
|
|
5.1.5. Теорема о среднем.
|
|
Теорема
Доказательство: Геометрический смысл формулы. Рис.1 При Следствие: Данное свойство позволяет оценить величину определенного интеграла. |
|
|

 , где
, где 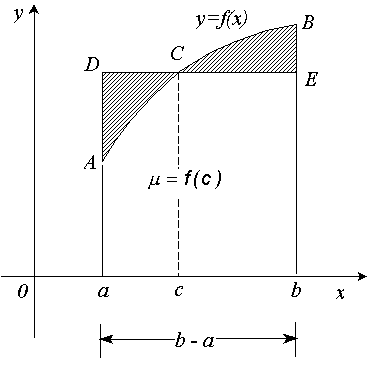
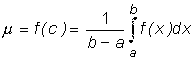 .
.