| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Определенный интеграл. Основные понятия. |
|
|
|
|
|
5.1.3. Основные теоремы. |
|
Интеграл,
как функция верхнего предела.
Замечание: Обозначение переменной интегрирования в определённом интеграле
никакой роли не играет, то есть:
Если функция интегрируема на некотором отрезке, то она ограничена
на нем. (Без доказательства).
Используя понятие
интеграла, как функции верхнего
предела, приведем еще одно доказательство формулы Ньютона
- Лейбница: То есть
|
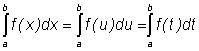
 есть некоторая функция от x.
есть некоторая функция от x.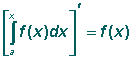 .
.
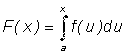 , то
, то 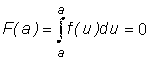 и
и 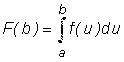 .
.  .
.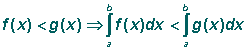 .
.
