| Темы | Предыдущий пункт | Следующий пункт | Литература | |||||
|
|
|||||

Определённый интеграл. Основные понятия. |
|||||
|
|
|||||
|
5.1.1. Вычисление определённого интеграла. Формула Ньютона-Лейбница |
|||||
|
В начале XVII века Ньютон и Лейбниц указали общий метод вычисления определенных интегралов путем сведения таких задач к отысканию первообразной функции.
где F(x) - есть первообразная функции f(x).
Доказательство: Запишем:
Согласно теореме Лагранжа о среднем:
Пример 1:
Пример 2: | |||||
|
|
|
|


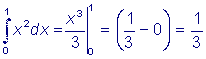 .
. 