2.1.7
Уравнение пучка прямых.
Совокупность всех прямых
плоскости, проходящих через некоторую
точку  , называется пучком прямых с
центром S. В аналитической геометрии
часто встречается потребность, зная
уравнения двух прямых пучка, найти
уравнение некоторой третьей прямой
того же пучка
при условии, что направление этой
прямой так или иначе описано. Задачи
такого типа можно решать, используя,
например, уравнение: , называется пучком прямых с
центром S. В аналитической геометрии
часто встречается потребность, зная
уравнения двух прямых пучка, найти
уравнение некоторой третьей прямой
того же пучка
при условии, что направление этой
прямой так или иначе описано. Задачи
такого типа можно решать, используя,
например, уравнение:
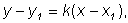
где в качестве 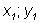 следует брать координаты центра пучка следует брать координаты центра пучка
 (угловой коэффициент
k
находится соответственно тому, как
задано направление искомой прямой).
Координаты центра
(угловой коэффициент
k
находится соответственно тому, как
задано направление искомой прямой).
Координаты центра  предварительно приходится
вычислять.
предварительно приходится
вычислять.
Следующее предложение
позволяет в подобных случаях избегать
вычисления координат  . .
Пусть 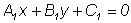 и
и 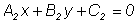 - уравнение двух прямых,
пересекающихся в точке S, а - уравнение двух прямых,
пересекающихся в точке S, а 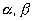 – какие угодно числа не
равные одновременно 0, тогда: – какие угодно числа не
равные одновременно 0, тогда:
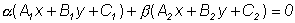
|
(1) |
есть уравнение прямой,
проходящей через точку S.
Доказательство.
Прежде всего установим,
что соотношение (1) есть действительно
уравнение. Для этого запишем его в виде
 |
(2) |
и докажем, что величины 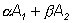 и
и  не
могут быть обе равными 0. Предположим
противное, т.е. что
не
могут быть обе равными 0. Предположим
противное, т.е. что 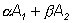 =
0 и =
0 и  =
0. Но тогда: =
0. Но тогда:
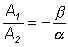 и
и 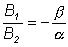 . .
Так как числа 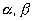 не равны
0
одновременно, то отношение не равны
0
одновременно, то отношение 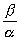 не может быть
неопределенным. Поэтому из предыдущих
равенств следует пропорция
не может быть
неопределенным. Поэтому из предыдущих
равенств следует пропорция 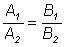 . .
Однако коэффициенты 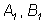 не могут быть пропорциональными
коэффициентам не могут быть пропорциональными
коэффициентам 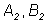 т.к. данные прямые
пересекаются. Таким образом, наше
предположение приходится отвергнуть.
Итак,
т.к. данные прямые
пересекаются. Таким образом, наше
предположение приходится отвергнуть.
Итак, 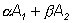 и и
 одновременно исчезнуть не
могут, а это означает, что равенство (1)
есть уравнение. Оно является
уравнением первой степени и,
следовательно, определяет некоторую
прямую. Остается доказать, что эта
прямая проходит через точку S. Пусть
одновременно исчезнуть не
могут, а это означает, что равенство (1)
есть уравнение. Оно является
уравнением первой степени и,
следовательно, определяет некоторую
прямую. Остается доказать, что эта
прямая проходит через точку S. Пусть
 -
координаты точки S. Так как каждая из
данных прямых проходит через точку S, то -
координаты точки S. Так как каждая из
данных прямых проходит через точку S, то и
и  ,
откуда: ,
откуда:
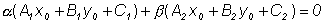 . .
Мы видим, что координаты
точки S удовлетворяют уравнению (1),
следовательно, прямая, определяемая
уравнением (1), проходит через точку S, и
наши предположения доказаны.
Таким образом, уравнение вида (1) при всяких
значениях 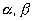 не равных одновременно
0,
определяет прямые пучка с центром S. не равных одновременно
0,
определяет прямые пучка с центром S.
Если 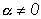 ,
то полагая ,
то полагая  ,
получим из уравнения (1): ,
получим из уравнения (1):
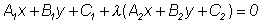 |
(3) |

Пример. Даны две прямые 2х + 3у – 5 =
0, 7х + 15у + 1 = 0, пересекающиеся в точке S.
Составить уравнение прямой, которая
проходит через точку S
и перпендикулярна прямой 12х – 5у – 1 = 0.
Решение.
Проверим утверждение
условия задачи: данные прямые
действительно пересекаются, т.к:
 . .
Далее составим уравнение
пучка прямых с центром S.
 |
(4) |
Представим уравнение (4) в
виде:
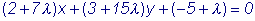 |
(5) |
Чтобы выделить в этом
пучке искомую прямую, вычислим 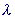 согласно условию перпендикулярности
этой прямой к прямой 12х – 5у – 1 = 0.
согласно условию перпендикулярности
этой прямой к прямой 12х – 5у – 1 = 0.
Найдем угловой
коэффициент искомой прямой:

Данная прямая имеет угловой
коэффициент 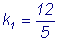 .
По условию
перпендикулярности .
По условию
перпендикулярности  ,
то есть ,
то есть  ,
откуда ,
откуда 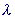 =
- 1. =
- 1.
Подставляя 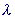 =
- 1 в уравнение (5) получаем -5х – 12у – 6 = 0 или 5х + 12у + 6 = 0. =
- 1 в уравнение (5) получаем -5х – 12у – 6 = 0 или 5х + 12у + 6 = 0.
 Задачи
для самостоятельного решения. Задачи
для самостоятельного решения.

| 