| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Дифференциальные уравнения высших порядков |
|
|
|
|
|
6.2.2. Некоторые типы дифференциальных уравнений, допускающих понижение порядка 1) Уравнения, не содержащие в своей записи искомую функцию y |
|
|
Метод решения рассмотрим на примере уравнения второго порядка. Уравнение вида  не содержит явным образом искомой функции y . Порядок такого
уравнения может быть понижен. Действительно, положим
не содержит явным образом искомой функции y . Порядок такого
уравнения может быть понижен. Действительно, положим
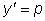 . Тогда . Тогда  . . Подставляя эти выражения производных в рассматриваемое уравнение, получим уравнение первого порядка 
относительно неизвестной функции p от x . Проинтегрировав это уравнение, находим его общее решение  , а затем из соотношения , а затем из соотношения
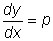
получаем общий интеграл исходного уравнения:  . . Аналогично можно понизить порядок у дифференциальных уравнений (n)-го порядка. Пример
Решить уравнение |
|
|
2) Уравнения, не содержащие аргумента искомой функции x |
|
Метод решения опять рассмотрим на примере уравнения второго порядка. Уравнение вида
Пример
Найти частное решение уравнения |
|
|
|
|
 .
.
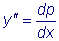
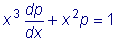 .
.
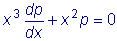 ,
,  .
. ,
т.е.
,
т.е. 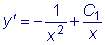 .
Следовательно,
.
Следовательно,
 .
. 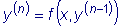 .
.
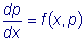 .
.
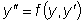 не содержит явным образом независимую переменную x . Порядок
этого уравнения также может быть понижен. И в этом случае полагаем
не содержит явным образом независимую переменную x . Порядок
этого уравнения также может быть понижен. И в этом случае полагаем
 ,
но теперь мы будем считать p функцией от y (а не от
x , как прежде).
Тогда
,
но теперь мы будем считать p функцией от y (а не от
x , как прежде).
Тогда  .
. 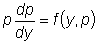 .
.
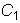 :
:
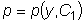 . Вспоминая, что
. Вспоминая, что  ,
, 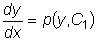 .
.
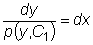 .
. 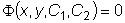 .
.  ,
, 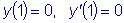 .
. 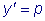 , рассматривая p как
функцию от y . Тогда
, рассматривая p как
функцию от y . Тогда 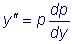
 .
.  .
. 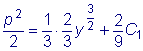
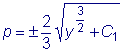 ,
,  .
. 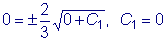 .
.  .
. 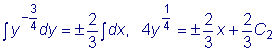
 .
. 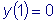 , найдем
, найдем
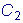 :
:
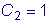 .
Искомое частное решение запишется:
.
Искомое частное решение запишется:  .
.