| Темы | Предыдущий пункт | Следующая лекция | Литература | |
|
|
|

Дифференциальные уравнения первого порядка |
|
|
|
|
|
6.1.5. Уравнения в полных дифференциалах |
|
Уравнением в полных дифференциалах называется уравнение вида
левая часть которого есть полный дифференциал некоторой функции
Переписав исходное уравнение в виде
таким образом
Необходимое и достаточное условие того, что левая часть уравнения является полным дифференциалом некоторой функции, выражается равенством
Функция
Пример
Проинтегрировать дифференциальное уравнение
Для данного уравнения
Так как выполнено условие (#), то данное уравнение является уравнением
в полных дифференциалах, следовательно,
Интегрируя первое из этих уравнений ( y при этом считается
постоянным), находим
где
Дифференцируя по y функцию U(x,y) = C
и принимая во внимание значение
Итак, общий интеграл данного уравнения:
Замечание.
Это уравнение является также однородным и его можно проинтегрировать
другим способом. |
|
|
|
|
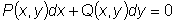 ,
,
 , т.е.
, т.е.
 .
.
 , заключим, что общий
интеграл этого уравнения определяется формулой
, заключим, что общий
интеграл этого уравнения определяется формулой
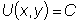 .
Как известно, полный дифференциал функции
.
Как известно, полный дифференциал функции
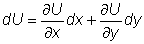 .
.
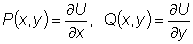 .
.
 . (#)
. (#)
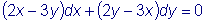 .
.
 .
.
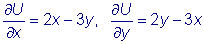 .
.
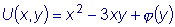 ,
,
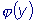 - функция подлежащая определению.
- функция подлежащая определению.
 ,
,
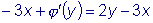 ,
,
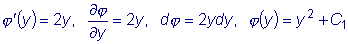 .
.
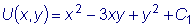 .
.

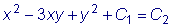
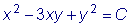 ,
,
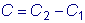 .
.