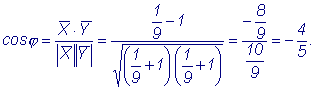| Темы | Предыдущий пункт | Следующий пункт | Литература | ||||||||||||
|
|
||||||||||||

Векторная алгебра |
||||||||||||
|
1.2.7 Скалярное произведение двух векторов. Возможны две операции умножения двух векторов. Одна дает в результате скаляр и поэтому называется скалярным умножением. Другая дает в результате вектор и поэтому называется векторным умножением. Рассмотрим сначала скалярное умножение, начав с приводящего к нему понятия работы.
Пусть постоянная
сила
Таким образом, двум
векторам - силе
Скалярным произведением двух векторов называется произведение их модулей на
косинус угла между ними.
Обозначение скалярного произведения возможно одним из трех способов: В дальнейшем изложении будем следовать обозначению
Таким образом, на основании определения Из (2.2) следует, что скалярное произведение двух векторов равно нулю тогда и только тогда,
когда хотя бы один из перемножаемых векторов равен нулю или когда эти
векторы перпендикулярны. Поэтому условие
Используя
определение проекции вектора на ось, можно скалярное произведение
представить в виде:
Скалярное произведение равно произведению модуля одного вектора на проекцию
другого на первый. Законы скалярного умножения Непосредственно из определения скалярного умножения и из формул (2.3) следует, что
алгебраические законы умножения чисел полностью сохраняются и для
скалярного умножения векторов: 1) Закон переместительности
2) Закон распределительности
3) Закон сочетательности относительно скалярного множителя
Скалярный квадрат
вектора равен квадрату его модуля. Действительно, Скалярное
произведение в координатной форме Легко показать, что
для скалярного произведения ортов имеют место следующие равенства: Используя эти
соотношения, получим запись скалярного произведения в
координатной форме. Пусть два вектора
Перемножив почленно, мы получим отсюда, в силу
правила перемножения ортов, следует: Итак, скалярное
произведение двух векторов равно сумме произведений соответствующих
проекций. В частности, скалярный квадрат вектора равен сумме квадратов
его проекций Отсюда получаем
формулу для вычисления длины вектора: Из определения
скалярного произведения двух векторов получим формулу для вычисления
угла между двумя векторами: Пример 1. При каком значении m векторы Решение: Находим скалярное
произведение этих векторов
Отсюда
7m - 28 = 0 и m = 4. Ответ: m = 4. Пример 2. Вычислить скалярное произведение
Решение: Используя свойства скалярного умножения: Ответ: - 5. Пример 3. Какой угол образуют единичные векторы
Решение: Из условия перпендикулярности двух векторов имеем
Ответ: Пример 4. Определить угол между векторами Решение:
Имеем: Следовательно: Ответ:
Пример 5. Раскрыть скобки в выражении Решение: Ответ: 2 . Пример 6. В одной и той же точке приложены две силы
Решение: Следовательно, Ответ: Пример 7. Даны векторы
Решение: Поскольку Ответ: |
|
|
|
|
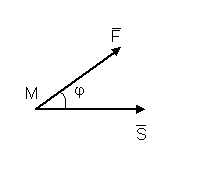 Рис. 2.15
Рис. 2.15
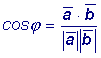 .
.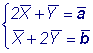 .
.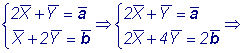
 .
.