| Темы | Предыдущий пункт | Следующий пункт |Литература | |
|
|
|

Векторная алгебра |
|
|
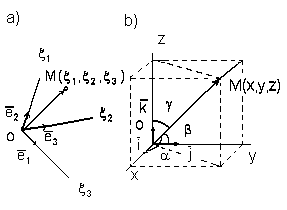
1.2.5. Система координат в пространстве. Аффинные координаты точки
Определение 1. Аффинная система координат в
пространстве определяется заданием
базиса
Определение 2.
Аффинными координатами любой точки М называются координаты вектора
Так как каждый
вектор
При решении задач чаще используются декартовы прямоугольные координаты. Декартова прямоугольная система координат является частным случаем аффинной системы. Декартовы прямоугольные координаты Определение 3.
Совокупность фиксированной точки O (начало координат) и
ортонормированного базиса
Прямые Ox, Oy и Oz, проходящие через начало координат в направлении базисных векторов
Плоскости, проходящие через оси координат, называются координатными плоскостями. Они делят пространство на восемь областей - октантов. Координатами точки М
называются координаты радиуса - вектора
Определение 4.
Декартовы прямоугольные координаты x, y и z вектора
Обозначим через Используя
определение проекций получим следующие формулы для координат x, y и z
вектора
Так как квадрат
диагонали прямоугольного параллелепипеда равен сумме квадратов трех его
измерений, то получим следующее выражение для длины вектора
Направляющие косинусы вектора можно выразить формулами:
Легко проверить
справедливость формулы:
|
|
|
|
|