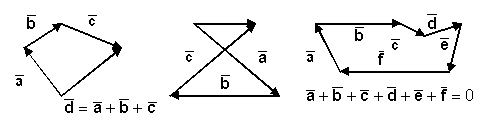| Темы | Предыдущий пункт | Следующий пункт |Литература | ||||
|
|
||||

Векторная алгебра |
||||
|
1.2.2 Линейные операции над векторами. Линейными операциями над векторами понимают операции сложения и вычитания векторов и умножение вектора на число. 1. Сложение векторов.
Определение 1.
Суммой
Пример 1.
Построить вектор
Решение:
Строим вектор
Дано: Построение:
Правило сложение двух векторов, получаемое из определения суммы векторов обычно называют "правилом треугольника".
Из определения суммы
можно получить правило сложения для неколлинеарных векторов, именуемое
"правилом параллелограмма", если вектор
Определение 2. Суммой При сложении более чем двух векторов используется "правило многоугольника": Определение 3. Суммой нескольких векторов называется вектор, соединяющий начало первого вектора с концом последнего, при условии, что начало каждого последующего вектора совпадает с концом предыдущего (рис. 2.7.).
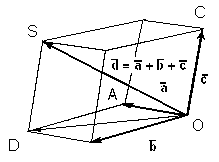
Рис. 2.7. Для сложения трех некомпланарных векторов удобно пользоваться "правилом параллелепипеда” (рис.2.8.).
Пусть надо найти
сумму некомпланарных векторов
Отложим от
произвольной точки О векторы
Сложение векторов обладает следующими свойствами:
1)
2)
3) существует нулевой вектор
4) для каждого вектора
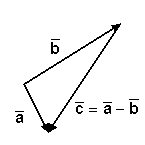
Справедливость свойств 1) - 4) вытекает из правил сложения векторов. 2. Вычитание векторов Определение 4. Разностью
С помощью свойств 1)
- 4) элементарно доказывается, что существует, и притом единственный,
вектор
Из этого определения
и из "правила треугольника" сложения векторов вытекает следующее правило
построения разности
Разность
Заметим, что
разностью 2-х векторов
3. Умножение вектора на число Определение 5.
Произведением вектора
1) модуль, равный
2) направление,
одинаковое с вектором
Законы умножения вектора на число:
1)
2)
3)
Определение 6. Необходимым и достаточным условием коллинеарности векторов
Вектор,
противоположный вектору Определение 7. Ортом
Пример 2.
Какому условию
должны удовлетворять неколлинеарные векторы
Решение:
По "правилу параллелограмма" векторы
Ответ:
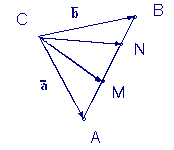
Пример 3.
В треугольнике АВС
сторону АВ точками M и N разделили на три равные части: AM
= MN = NB.
Выразить вектор
Решение: Из определения суммы
Ответ:
Пример 4. Даны три ненулевых вектора
Решение: Так как
Аналогично,
или Следовательно,
Но векторы
Отсюда,
Ответ:
|
|
|
|
|
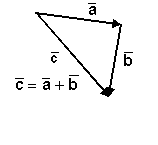 Рис. 2.4
Рис. 2.4
 Рис.
2.6.
Рис.
2.6.