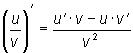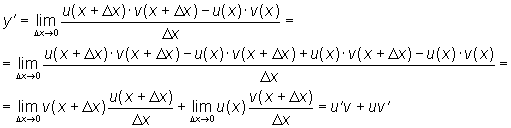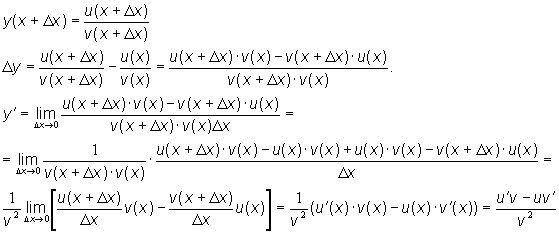| Темы | Предыдущий пункт | Литература | |
|
|
|

Производная и дифференциал |
|
|
|
|
3.2.5. Основные правила дифференцирования |
||||||||||
|
Применяя общий способ нахождения
производной с помощью предела можно
получить простейшие формулы
дифференцирования. пусть u = u(x), v = v(x)
- две дифференцируемые функции от
переменной x.
Доказательство формулы 3. Пусть y = u(x) + v(x). Для
значения аргумента x+ Тогда
Следовательно:
Доказательство формулы 4. Пусть y = u(x) v(x). Для
значения аргумента x+ Тогда
Заметим, что поскольку
каждая из функций u и v дифференцируема
в точке x, то они непрерывны в этой точке,
а значит: Поэтому можем записать:
Доказательство формулы 5. Пусть
Примеры: 1. 2. 3. Таким образом:
Аналогично выводится:
|
|
|
|
|