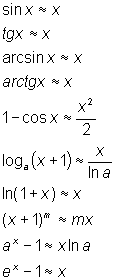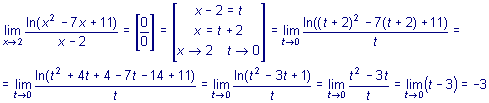| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Предел. Непрерывность функции. |
|
|
|
|
|
3.1.9. Сравнение бесконечно малых функций
|
|
Пусть при
Если
Примеры 1. Пусть f(x)=x2,g(x)=5x. Функции
являются бесконечно малыми при
Следовательно, f(x) – бесконечно малая высшего порядка относительно g(x). 2. Пусть f(x)=x2–4,g(x)=x2–5x+6 – бесконечно малые при Поэтому f(x) и g(x) одного порядка. 3. f(x)=tg2x, g(x) = 2x – бесконечно малые при
Следовательно, f(x) и g(x) эквивалентны. 4.
– этот предел не существует. Поэтому говорят, что функции f и g не сравнимы.
При вычислении пределов полезно помнить о следующем свойстве эквивалентных бесконечно малых функций. Теорема. Пусть f и g – бесконечно малые функции
при Доказательство. Имеем
что и требовалось доказать. Следующие бесконечно
малые функции эквивалентны при
Примеры 1.
2.
|
|
|
|
|