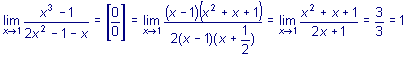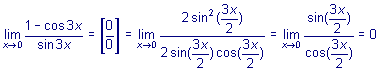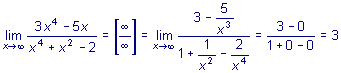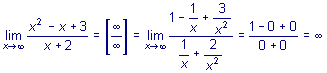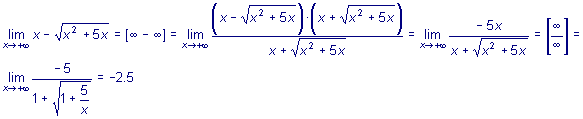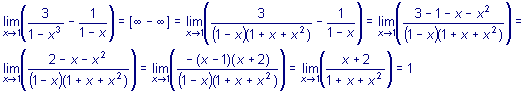| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Предел. Непрерывность функции. |
|
|
|
|
|
3.1.7. Типы неопределенностей и способы их раскрытия |
|
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Условные выражения
характеризуют типы неопределенностей и применяются для обозначения переменных величин, при вычислении предела которых нельзя сразу применять общие свойства пределов. Рассмотрим некоторые приемы раскрытия неопределенностей. I. Неопределенность
Примеры 1.
2.
3.
4.
II. Неопределенность Примеры
1.
2.
При вычислении пределов числитель и знаменатель дроби разделили на x в старшей степени.
Следующие виды неопределенностей с помощью алгебраических
преобразований функции, стоящей под знаком предела, сводят к одному из
рассмотренных выше случаев III. Неопределенность
Пример
IV. Неопределенность
Пример ы1. 2.
|
|
|
|
|