| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Предел. Непрерывность функции. |
|
|
|
|
|
3.1.5. Теоремы о пределах |
|
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.
Доказательство. Проведем доказательство для двух слагаемых, так
как для любого числа слагаемых оно проводится так же. Пусть
Так как b + c есть постоянная величина, а
Пример
Доказательство. Пусть Произведение
bc есть величина постоянная. Функция Следствие 1. Постоянный множитель можно выносить за знак
предела: Следствие 2. Предел степени равен степени предела:
Пример :
Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е
Доказательство. Пусть
Дробь
Пример ы:1. 2. Рассмотрим Теорема 4. Пусть даны три функции f(x), u(x) и v(x), удовлетворяющие неравенствам u(x)≤f(x)≤ v(x). Если функции u(x) и v(x) имеют один и тот же
предел при Смысл этой теоремы понятен из рисунка.
Теорема 5. Если при Теорема 6. Если две функции f(x) и g(x) при всех
значениях аргумента x удовлетворяют неравенству f(x)
> g(x) и
имеют пределы |
|
|
|
|
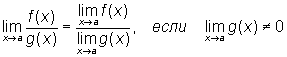
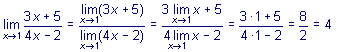
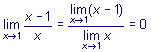 , т.е.
, т.е.
