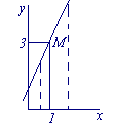| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|
 Предел.
Непрерывность функции.
Предел.
Непрерывность функции.
|
|
|
|
|
|
3.1.3. Предел функции |
|
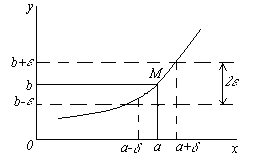
Пусть функция y= f (x) определена в некоторой окрестности
точки a. Предположим, что независимая переменная x
неограниченно приближается к числу a. Это означает, что мы
можем придавать х значения сколь угодно близкие к a,
но не равные a. Будем обозначать это так
Введем строгое определение предела функции. Функция y
= f (x) стремится к пределу b при Если b
есть предел функции f(x) при
или Проиллюстрируем это определение на графике функции. Т.к. из
неравенства |x - a| <
Несложно заметить, что предел функции должен обладать теми же
свойствами, что и предел числовой последовательности, а именно
Пример
Найти предел функции y
= 2x + 1 при
Используя график функции, можно увидеть, что если
Докажем это.
Понятие предела функции в бесконечно удаленной точке До сих пор мы рассматривали пределы для случая, когда переменная величина x стремилась к определенному постоянному числу. Будем говорить, что переменная x стремится к бесконечности, если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х = х0, начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x| > M. Например, пусть переменная х принимает значения x1= –1, x2=2, x3= –3, …, xn=(–1)nn, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M. Переменная величина Аналогично, Будем говорить, что функция f(x) стремится к пределу
b
при
Пример
Используя определение, доказать, что
Нужно доказать, что при произвольном
будет
выполняться неравенство Бесконечно большие функции Ранее мы рассмотрели случаи, когда функция f(x) стремилась к
некоторому конечному пределу b при
Рассмотрим теперь случай, когда функция y=f(x) стремится к бесконечности при некотором способе изменения аргумента. Функция f(x) стремится к бесконечности при
Если f(x) стремится к бесконечности при
Ограниченные функции Пусть задана функция y=f(x), определенная на некотором множестве D значений аргумента.
Функция y=f(x) называется ограниченной на множестве D, если существует положительное число М такое, что для всех значений x из рассматриваемого множества, выполняется неравенство |f(x)|≤M. Если же такого числа М не существует, то функция f(x) называется неограниченной на множестве D. Примеры:
Функция y = f(x) называется ограниченной
при Функция y = f(x) называется ограниченной
при Установим связь между ограниченной функцией и функцией, имеющей предел.
Теорема Если Замечание. Из определения ограниченной функции следует, что если
|
|
|
|
|