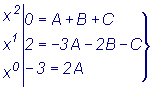| Темы | Предыдущий пункт | Следующий пункт | Литература | |
|
|
|

Интегрирование рациональных функций |
|
|
|
||||
|
4.3.2. Разложение дробно-рациональной функции на простейшие дроби |
||||
|
Интегрирование рациональных дробей производится путем представления данных дробей в виде суммы простейших дробей. Простейшей дробью называется дробь одного из следующих четырех типов:
Интегралы от этих дробей находятся легко. Имеет место следующая теорема.
Для вычисления значений A, М, N в разложении функции R(х)
на сумму простейших рациональных дробей часто используют метод неопределенных
коэффициентов, суть которого заключается в следующем. С учетом вышеизложенной
теоремы данную дробь R(х) представим в виде суммы простейших рациональных
дробей с неопределенными коэффициентами Ai, Мi, Ni. Полученное равенство
является тождеством. Поэтому, если привести все дроби к общему знаменателю
Pn(x) в числителе получим многочлен В некоторых случаях с целью упрощения вычислений можно воспользоваться
следующим соображением. Так как многочлены Пример Разложим дробь В соответствии с формулой (3) разложение на элементарные дроби имеет
вид Теперь найдем коэффициенты разложения методом частных значений. Подставим в числитель (1) вместо х частные значения, равные корням знаменателя x = 0, x = 1, x = 2.Получим равенства -3 = 2A, -1 = -B, 1 = 2C. Получим те же значения коэффициентов. Теперь можно будет использовать это разложения для нахождения интеграла. В следующем разделе 4.3.3 мы это сделаем. |
||||
|
|
|
|

 . Интегралы такого
вида находят с помощью рекуррентной формулы понижения степени знаменателя:
. Интегралы такого
вида находят с помощью рекуррентной формулы понижения степени знаменателя:

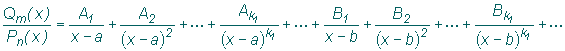
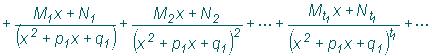
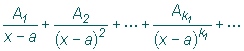 ,
а каждой паре комплексно-сопряженных корней кратности t1 множителя
соответствует сумма дробей вида
,
а каждой паре комплексно-сопряженных корней кратности t1 множителя
соответствует сумма дробей вида 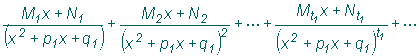 .
.