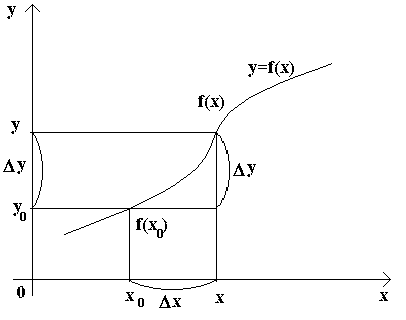
Пусть имеем некоторую функцию y= f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y = f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x₀ и новое x. Разность x - x₀ называется приращением аргумента x в точке x₀ и обозначается x. Таким образом, x = x - x₀ (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x₀+x, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x₀ значение функции было f(x₀), то в новой точке x функция будет принимать значение f(x) = f(x₀ +x).

Разность y – y₀ = f(x) - f(x₀) называется приращением функции y = f(x) в точке x₀ и обозначается символом y. Таким образом,

y = f(x) - f(x0) = f(x0 +x) - f(x0).

(1)

Обычно исходное значение аргумента x₀ считается фиксированным, а новое значение x – переменным. Тогда y₀ = f(x₀) оказывается постоянной, а y = f(x) – переменной. Приращения y и x также будут переменными и формула (1) показывает, что y является функцией переменной x.

Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при . Если этот предел существует, то его называют производной данной функции f(x) в точке x₀ и обозначают f '(x₀). Итак,

Производной данной функции y = f(x) в точке x₀ называется предел отношения приращения функции y к приращению аргумента x, когда последнее произвольным образом стремится к нулю:

Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)

Производная обозначается символами f '(x), y ', . Конкретное значение производной при x = a обозначается f '(a) или .

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило:

1. Придать x приращение x и найти наращенное значение функции f(x + x).
2. Найти приращение функции y = f(x + x) – f(x).
3. Составить отношение и найти предел этого отношения при .